Water/Description: Difference between revisions
< Water
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
{{ComponentDescriptionTemplate | {{ComponentDescriptionTemplate | ||
|Status=On hold | |Status=On hold | ||
|Reference=Crop and grassland model | |Reference=Biemans, 2012; Rost et al., 2008; Gerten et al., 2004; Biemans et al., 2011; Nilsson et al., 2005; Alcamo et al., 2003; Davies et al., 2013; Pastor et al., 2013; | ||
|Description=The LPJmL model simulates the global carbon and water balances as part of the dynamics of natural vegetation and agricultural production systems. Because of the coupling of LPJmL to IMAGE, the carbon cycle, natural vegetation, crop production ([[C cycle and natural vegetation dynamics]] and [[Crop and grassland model]]), land-use allocation ([[Forest management]]) and hydrology can be modelled in a consistent way. | |||
==The ‘natural’ hydrological cycle== | |||
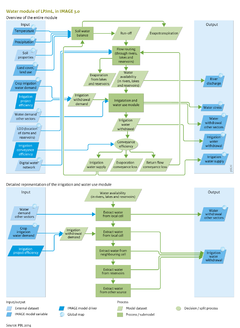
The hydrological module in the LPJmL model consists of a vertical water balance (Gerten et al., 2004) and a lateral flow component ([[Rost et al., 2008]]) (Figure 6.3.1a[[*********]]), which are run at 0.5 degree resolution in time steps of one day. The soil in each grid cell is represented by a two-layer soil column of 0.5 and 1 metre depth, respectively, partly covered with natural vegetation or crops. | |||
The potential evaporation rate in each grid cell depends primarily on net radiation and temperature, and is calculated using the Priestley-Taylor approach ([[Gerten et al. 2004]]). The actual evapotranspiration is calculated as the sum of three components: evaporation of intercepted precipitation, bare soil evaporation and plant transpiration. ([[Gerten et al., 2004]]). | |||
The water storage in the canopy is a function of vegetation type, leaf area index ([[LAI]]) and precipitation amount. Interception evaporation occurs at potential evaporation rate, during the fraction of the daytime that the canopy is wet. | |||
Plant transpiration is modelled as the minimum of atmospheric demand and plant water supply. Plant water supply depends on the plant-dependent maximum transpiration rate and relative soil moisture. Soil evaporation occurs in the fraction of land in the grid cell that is not covered by vegetation. Soil evaporation equals potential evaporation when the soil moisture of the upper 20 cm is at field capacity, and declines linearly with relative soil moisture. | |||
Precipitation reaching the soil (throughfall, precipitation minus interception) either accumulates as snow (if T<0 °C) or (if T>0 °C) infiltrates into the soil. Snowmelt is calculated using a simple degree-day method ([[Gerten et al., 2004]]). | |||
The soil is parameterised as a simple bucket model. The status of soil moisture of the two soil layers is updated daily, accounting for throughfall, snowmelt, evapotranspiration, percolation and runoff. Percolation rates for the two soil layers depend on soil type and decline exponentially with soil moisture. Total runoff is calculated as the excess water above field capacity from the two soil layers and the water percolating through the second soil layer. The current version of the LPJmL model, has no explicit representation of groundwater recharge, but a simple groundwater scheme is under development. The annual runoff includes the sustainable amount of groundwater, but without any time delay. | |||
All runoff is routed through a gridded river network, representing a system of rivers, naturally formed lakes and reservoirs, using a simple routing algorithm ([[Rost et al., 2008]]). The local runoff is added to the surface water storage in the cell, and is subsequently flowing downstream with a constant flow velocity of 1 m s<sup>-1</sup> until it reaches a lake or reservoir. Water accumulates in the lakes and reservoirs, and outflow depends on the actual storage relative to the maximum storage capacity (for lakes) and the operational purpose of the reservoir (for man-made reservoirs, see the next section) ([[Biemans et al., 2011]]) | |||
==Human interactions with the global water cycle== | |||
===Irrigation and demand for irrigation water=== | |||
To simulate water availability and demand related to agriculture, the LPJmL model includes an irrigation algorithm ([[Rost et al., 2008]]) and one that simulates the operation of large reservoirs to supply water to irrigated areas ([[Biemans et al., 2011]]). | |||
The irrigation demand module (Figure 6.3.1.b[[*********]]) is described in detail by [[Rost et al., 2008]]. The crop irrigation demand for an irrigated crop is defined as the minimum of atmospheric evaporative demand and the amount of water needed to fill up the soil to field capacity. The irrigation withdrawal demand is subsequently calculated as the product of the crop irrigation demand and a country-specific irrigation efficiency factor that reflects the type of irrigation system ([[Rost et al., 2008]]). Irrigation water is extracted from the rivers and lakes in the grid cell or a neighbouring grid cell. If those local surface water sources cannot satisfy the total demand, water will be extracted from nearby reservoirs, if available. Finally, water can be supplied from an unlimited source of water that can be interpreted as non-sustainable groundwater or water imported from another basin. | |||
By subsequently excluding these water sources in a series of model runs, it is possible to attribute irrigation water supply and crop production to different sources of water. | |||
Some of the water withdrawn for irrigation is lost during transport from withdrawal point to irrigated field. The magnitude of these losses depends on the type of conveyance system (e.g. open channel or pipeline) and is determined using a country-specific conveyance efficiency factor ([[Rost et al., 2008]]). Therefore, the amount of water applied to a field is always lower than the amount of water withdrawn, but in case of no water stress, still higher than the crop irrigation demand. | |||
===Large reservoirs=== | |||
Around 50% of global river systems are regulated by dams, and most of them are in basins where irrigation and economic activities take place ([[Nilsson et al., 2005]]). Approximately a third of all large dams primarily have been built for irrigation purposes. Therefore, to adequately estimate agricultural water use, the use of man-made reservoirs has been taken into account. | |||
The reservoir operation module of the LPJmL model ([[Biemans et al., 2011]]) distinguishes three types of reservoirs: | |||
#reservoirs that are primarily used for irrigation; | |||
#reservoirs that are primarily used for other purposes (e.g. hydropower, flood control) but are also used for irrigation; | |||
#reservoirs that are not used for irrigation. | |||
The management of these reservoirs varies per type. The outflow of irrigation reservoirs follows the temporal pattern of irrigation demand, whereas the other reservoirs are intended to release their water in equal amounts throughout the year. Water from irrigation reservoirs is supplied to downstream irrigated areas (for details, see [[Biemans et al., 2011]]). | |||
==Water demand in other sectors== | |||
The IMAGE-LPJmL model only calculates agricultural water demand internally, hence water demand in other sectors (household, livestock, manufacturing and electricity) is calculated separately. For household and manufacturing sectors data and algorithms are adopted from the WaterGAP model ([[Alcamo et al., 2003]]). For the electricity sector, a process-based estimation is used, based on the study by ([[Davies et al., 2013]]), and livestock demand follows from the number of heads, estimated in the livestock production model (see [[Livestock systems]]), with the water demand per head adjusted for climate conditions. Domestic demand is a function of population size and per-capita income, corrected for the share of the population without access to a piped water supply (see [[Human Development]]). Manufacturing demand is a function of industrial value added, corrected for changes in sector composition; for example, the structural change factor also used for energy demand (see Section 4.1.1). For the electricity sector, a technology-based approach was adopted from the study by ([[Davies et al., 2013]]). The type of power plant (e.g. standard steam cycle, combined steam cycle) determines the demand for cooling capacity. Cooling demand is also corrected for cogeneration of heat and power, as those plants require far less cooling capacity. In addition, the type of cooling facility in place determines how much water is required. Once-through cooling systems use large volumes of surface water that are returned almost entirely to the water body that they were extracted from, albeit at an elevated temperature. Wet cooling towers exploit the evaporation heat capacity of water and, hence, require much lower water volumes. However, a significant part of the cooling water evaporates during the process and does not return to the original water body. In some regions, cooling ponds are used, where cooling water is pumped and recycled in a closed loop, with water demand characteristics somewhere in-between the once-through and wet tower cooling systems. Finally, dry cooling systems are deployed that use air as a coolant and, therefore, require no cooling water at all. Based on data from ([[Davies et al., 2013]]), market shares of types of cooling systems – for each power plant type distinguished in TIMER, in each world region – are combined with energy input requirements to arrive at the total water demand for the electricity sector. | |||
In the LPJmL model, the water needed in other sectors is extracted from local surface waters, if available (rather than from reservoirs). Meeting the demand from these sectors receives priority over water withdrawal for irrigation. | |||
The current version of IMAGE-LPJmL does not take into account the water needs of ecosystems, or other uses, such as shipping or recreation. However, a new module to calculate environmental flow requirements is under development ([[Pastor et al., 2013]]). By using this module, water withdrawals will be constrained so that a minimal environmental flow is guaranteed, and the module also will be used to identify possible areas of conflict between water users. | |||
===Impact indicators=== | |||
Water stress is often presented as a spatially and temporally averaged water withdrawal-to-availability ratio, typically at basin or country level. The amount of people living under water stress is estimated by overlaying a water-stress map with one of population density. Those indicators are used to present IMAGE-LPJmL results (e.g. in the OECD Environmental Outlook, see Figure 6.3.2[[*******]]) but they mask the potential occurrence of water shortages on a short-term or sub-basin scale. Therefore, water stress should also be calculated at higher spatial and temporal resolutions (see e.g. [[Biemans, 2012]]). | |||
The impacts of water stress differ per sector, but the above described indicators do not provide insight into those impacts. Apart from the general water stress indicators, the model also considers production reductions in irrigated agriculture due to limited water availability as an indicator of agricultural water stress ([[Biemans, 2012]]). | |||
}} | }} | ||
Revision as of 11:13, 10 December 2013
Parts of Water/Description
| Component is implemented in: |
|
| Related IMAGE components |
| Projects/Applications |
| Key publications |
| References |