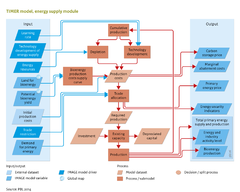
Energy supply/Description
Parts of Energy supply/Description
| Component is implemented in: |
|
| Related IMAGE components |
| Projects/Applications |
| Key publications |
| References |
Model description of Energy supply
Fossil fuels and uranium
Depletion of fossil fuels (coal, oil and natural gas) and uranium is simulated on the assumption that resources can be represented by a long-term cost-supple curve, consisting of different resource categories with increasing costs levels. The model assumes that the cheapest deposits will be exploited first. For each region, there are 12 resource categories for oil, gas and nuclear fuels, and 14 categories for coal.
A key input for each of the fossil fuel and uranium supply submodules is fuel demand (fuel used in final energy and conversion processes). Additional input includes conversion losses in refining, liquefaction, conversion, and energy use in the energy system. Upstream energy use is endogenously determined based energy carrier, region in which the energy carrier is produced, production rate, and resource category. These submodules indicate how demand can be met by supply in a region and other regions through interregional trade.
| Oil | Natural gas | Underground coal | Surface coal | |
|---|---|---|---|---|
| Cum. 1970-2015 production | 6.5 | 3.4 | 2.4 | 1.5 |
| Reserves | 9.4 | 7.3 | 17 | 3.6 |
| Other conventional resources | 33 | 17 | 481 | 56 |
| Unconventional resources (reserves) | 2.0 | 0.30 | ||
| Other unconventional resources | 54 | 2023 | ||
| Total | 105 | 2051 | 501 | 61 |
Fossil fuel resources are aggregated to five resource categories for each fuel (the table above). Each category has typical production costs. The resource estimates for oil and natural gas supply imply that for conventional resources supply is limited to only about 7 times the 1970–2015 production level. Production estimates for unconventional resources are much larger, albeit speculative. Recently, some of the occurrences of these unconventional resources have become competitive such as shale gas and tar sands. For coal, even current reserves amount to almost ten times the production level of the last three decades. For all fuels, the model assumes that, if prices increase, or if there is further technology development, the energy could be produced in the higher cost resource categories. The values presented in the table above represent medium estimates in the model, which can also use higher or lower estimates in the scenarios. The final production costs in each region are determined by the combined effect of resource depletion and learning-by-doing.
Trade
Trade is dealt with in a generic way for oil, natural gas and coal. In the fuel trade model, each region imports fuels from other regions. The amount of fuel imported from each region depends on the relative production costs and those in other regions, augmented with transport costs, using multinomial logit equations. Transport costs are calculated from representative interregional transport distances and time- and fuel-dependent estimates of the costs per GJ per kilometre.
To reflect geographical, political and other constraints in the interregional fuel trade, an additional 'cost' is added to simulate trade barriers between regions (this costs factor is determined by calibration). Natural gas is transported by pipeline or liquid-natural gas (LNG) tanker, depending on distance, with pipeline more attractive for short distances. In order to account for cartel behaviour, the model compares production costs with and without unrestricted trade. Regions that can supply at lower costs than the average production costs in importing regions are assumed to supply oil at a price only slightly below the production costs of the importing regions. Although also this rule is implemented in a generic form for all energy carriers, it is only effective for oil, where the behaviour of the OPEC cartel is simulated to some extent.
Renewable energy
IMAGE model the supply of eight renewable energy options: utility-scale photovoltaic (PV), rooftop PV, concentrated solar power (CSP), onshore wind energy, offshore wind energy, first-generation bio-energy, lignocellulosic bio-energy, and hydropower is estimated generically as follows (Hoogwijk, 2004; De Vries et al., 2007; Gernaat et al., 2017; Köberle et al., 2015; Gernaat et al., 2014; Daioglou et al., 2019; Gernaat):
Firstly, physical and geographical data are collected on a 0.5x0.5 degree grid. The characteristics of wind speed, insulation and monthly variation are taken from the digital databases.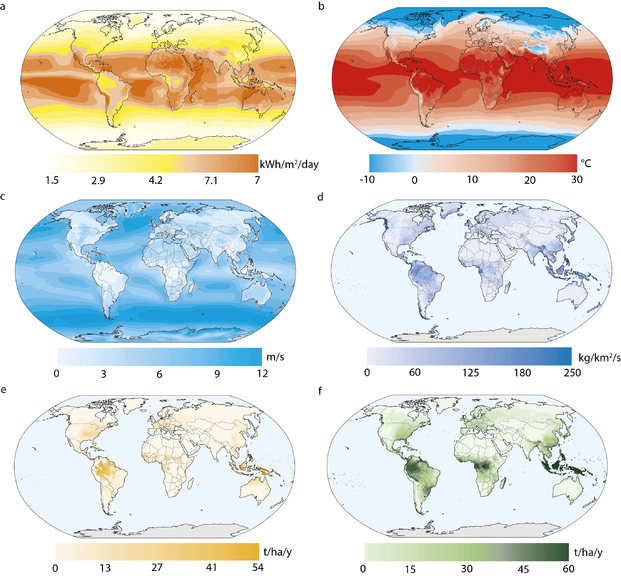
The methodology assumes that part of the grid cell can be used for energy production, given its physical–geographic (terrain, habitation) and socio-geographical (location, acceptability) characteristics. This leads to an estimate of the geographical potential. Several of these factors are scenario-dependent. The geographical potential for biomass production, for example, is estimated using suitability factors taking considering competing land-use options and the harvested rain-fed yield of energy crop. Next, we assume that only part of the geographical potential can be used due to limited conversion efficiency and maximum power density, This result of accounting for these conversion efficiencies is referred to as the technical potential. The final step is to relate the technical potential to on-site production costs. Information at grid level is sorted and used as supply cost curves to reflect the assumption that the lowest cost locations are exploited first. Supply cost curves are used dynamically and change over time as a result of the learning effect.
The calculation of each renewable energy potential is explained in detail in separate published articles. Here, a short explanation is given introducing each.
Utility-scale PV and CSP starts with the theoretical potential based on a global solar irradiation map (kWh m-2 day-1) (Hoogwijk, 2004; Köberle et al., 2015). This is subsequently restricted by excluding unsuitable areas (e.g. areas with snow cover or steep mountainous terrain) to calculate the geographical potential. The area that remains is further restricted by suitability factors. The idea behind suitability factors is that only part of the land is physically available for solar applications to ensure that it may keep the land-use function that it has, such as agricultural crop production. To calculate the technical potential, conversion efficiencies are assumed that are explained in method section ‘Climate impacts on renewable energy’.
Rooftop PV builds on the method of utility-scale PV, using the theoretical and technical aspects, but differentiates on the geographical potential (). For rooftop PV, the geographical potential is determined according to roof area. This area is estimated by dividing the living area per household by the number of floors per household, both of which are based on census data. The estimates distinguish between urban areas and rural areas, and are combined with an urban/rural population map to scale down the estimated roof areas to grid level. The technical calculations are similar as the ones used to calculate utility-scale PV and explained in method section ‘Climate impacts on renewable energy’.
Calculations of onshore and offshore wind energy potential start with wind speeds (m s-1) (Hoogwijk, 2004; Gernaat et al., 2014). Then, similar as for solar power, areas are excluded and further restricted according to suitability factors. For the remaining geographical area, based on wind data, the electricity output is calculated using a Weibull distribution function and power curve of the turbine. For details on offshore wind methodology see Supplementary Text 7-S2.
Bio-energy potential calculations start with primary biomass production, represented through yields (t ha-1 y-1) (Hoogwijk, 2004; Daioglou et al., 2019). Potential primary biomass sources include maize, sugar, and lignocellulosic crops (trees, switchgrass, and Miscanthus). Land availability for bio-energy production is limited by agricultural production following a ‘food-first’ principle where agricultural lands are determined first and are off-limits for biomass production. The technical potential is further limited by excluding forests, nature reserves and water stressed areas. In principle, bio-energy can be produced on remaining unprotected lands but also on abandoned agricultural lands. Besides energy crops, residues from agricultural and forestry can also be used as a feedstock. The costs of primary bio-energy crops are calculated with a Cobb-Douglas economic growth model using labour , land rent and capital costs as inputs [1]. The land costs are based on average regional income levels per km2, which was found to be a reasonable proxy for regional differences in land rent costs. The production functions are calibrated to empirical data .This technical potential is converted to several secondary energy carriers (solids, liquids, electricity, hydrogen) that compete in the energy system with other secondary energy carriers, such as fossil fuels or renewables (Daioglou et al., 2019) for a full description of biomass supply and demand in IMAGE) [2][3] [4].
Calculations of hydropower potential start with run-off (kg km-2 s-1) that flows from high elevation to low elevation (representing discharge). On the basis of these discharge maps, >3.8 million site-specific hydropower installations were evaluated, at a 25km interval for every river between 56° S and 60° N (the excluded area is due to unavailable topographic data). At each site, high-resolution topographic data (3” × 3”) were used to calculate the cost-optimal dam dimensions and associated production potential. In this way, 60,000 suitable sites were identified, which together represent the remaining technical potential (see Gernaat et al., 2017 for a full description of the site selection process).
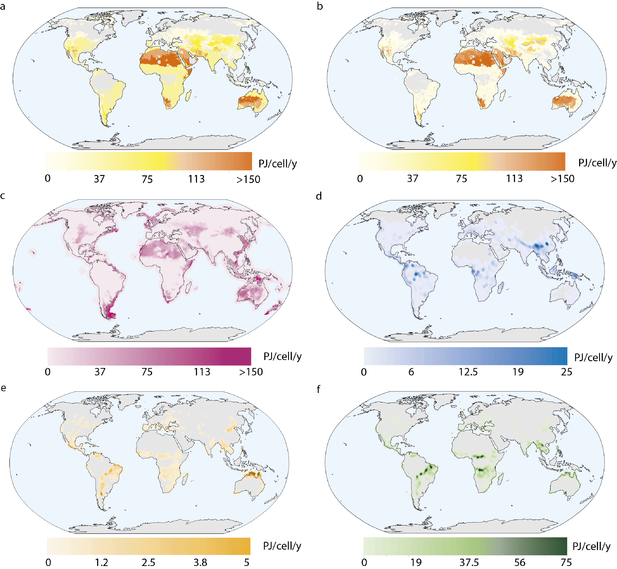
The maps on technical potential for all renewables are combined with economic information to generate cost-supply curves. Assumptions on cost can be found in the separate articles but the general methodology is as follows. Each technology requires an investment before it can produce energy. This investment (in USD) is divided by the annual production (kWh) to calculate the production cost (USD kWh-1). This yields two global maps, a technical potential map (kWh) and a production cost map (USD kWh-1). Together they are used to generate a cost-supply curve, by sorting (in ascending order) the cells in the production cost map while simultaneously adding the same cells from the technical potential map.
- ↑ The Cobb–Douglas production function is a particular functional form of the production function widely used to represent the technological relationship between the amounts of two or more inputs, particularly physical capital and labor, and the amount of output that can be produced by those inputs.
- ↑ Daioglou, V., Doelman, J.C., Wicke, B., Faaij, A. and van Vuuren, D.P., 2019. Integrated assessment of biomass supply and demand in climate change mitigation scenarios. Global Environmental Change, 54, pp.88-101.
- ↑ Daioglou, V., Stehfest, E., Wicke, B., Faaij, A. and Van Vuuren, D.P., 2016. Projections of the availability and cost of residues from agriculture and forestry. Gcb Bioenergy, 8(2), pp.456-470.
- ↑ Daioglou, V., Doelman, J.C., Stehfest, E., Müller, C., Wicke, B., Faaij, A. and van Vuuren, D.P., 2017. Greenhouse gas emission curves for advanced biofuel supply chains. Nature Climate Change, 7(12), p.920.