Water/Description: Difference between revisions
m (Text replace - "Livestock" to "Livestock systems") |
No edit summary |
||
| (17 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
{{ComponentDescriptionTemplate | {{ComponentDescriptionTemplate | ||
|Reference=Nilsson et al., 2005; Alcamo et al., 2003; Davies et al., 2013; Pastor et al., | |Reference=Nilsson et al., 2005;Alcamo et al., 2003;Davies et al., 2013;Pastor et al., 2014;Bondeau et al., 2007;Sitch et al., 2003;Gerten et al., 2004;Rost et al., 2008;Biemans et al., 2013 | ||
}} | |||
<div class="page_standard"> | |||
In IMAGE, the hydrological cycle is represented by LPJmL ([[Bondeau et al., 2007]]; [[Gerten et al., 2013]]; [[Schaphoff et al., 2018a]]), which simulates the global hydrological cycle as part of the dynamics of natural vegetation and agricultural production systems. Because LPJmL is linked to IMAGE, there is consistency in the way the [[Carbon cycle and natural vegetation|carbon cycle, natural vegetation]] dynamics, [[Crops and grass|crop growth and production]], [[land-use allocation]] and the water balance are modelled. | |||
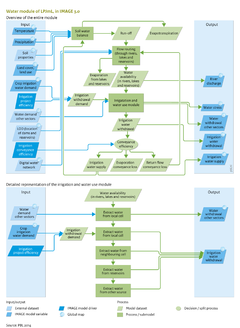
Data on annual [[land cover and land use]] are used as input to LPJmL, including information on the location of irrigated areas and crop types (Figure Flowchart and Input/Output Table at [[Water|Introduction part]]). This affects the amount of water that evaporates and runs off, as well as the amount of water needed for irrigated crops during the (simulated) growing season. Simultaneously, information on water availability and potential yields calculated by LPJmL is taken into account in the [[Land-use allocation]] model to identify suitable locations to expand irrigated areas. From the energy module, LPJmL receives water demands for industries, households and electricity. Together with water for irrigation these make up the total water demands in LPJmL. | |||
Climate is used as input in LPJmL to determine potential evapotranspiration, and the precipitation input to the water balance ([[Gerten et al., 2004]]). The [[Crops and grass]] module, which is also part of LPJmL, calculates irrigation water demand based on crop characteristics, soil moisture and climate. If the amount of water available for irrigation is limited, water stress will occur which leads to reduction of crop yields calculated by the [[Crops and grass|crop and grassland]] model. | |||
===The natural hydrological cycle=== | |||
The Hydrology module in LPJmL consists of a vertical water balance ([[Gerten et al., 2004]];[[Schaphoff et al., 2013]]) and a lateral flow component ([[Rost et al., 2008]]) that are simulated at 0.5 degree resolution in daily time steps (Figure Flowchart). The soil in each grid cell is represented by a five-layer soil column of 0.2, 0.3, 0.5, 1.0 and 1.0 m depth, partly covered with natural vegetation or crops. | |||
The potential evapotranspiration rate in each grid cell depends primarily on net radiation and temperature, and is calculated using the Priestley-Taylor approach ([[Gerten et al., 2004]]). The actual evapotranspiration is calculated as the sum of three components: evaporation of water stored in the canopy (interception), bare soil evaporation and plant transpiration ([[Gerten et al., 2004]]). Water storage in the canopy is a function of vegetation type, leaf area index ({{abbrTemplate|LAI}}) and precipitation amount. Plant transpiration is modelled as the minimum of atmospheric demand and plant water supply. Plant water supply depends on the plant-dependent maximum transpiration rate and relative soil moisture. Soil evaporation occurs in the proportion of land in the grid cell that is not covered by vegetation. It equals potential evaporation when the soil moisture of the upper 20 cm is at field capacity, and declines linearly with relative soil moisture. | |||
Precipitation reaching the soil (throughfall, precipitation minus interception) either accumulates as snow or infiltrates into the soil. Snowmelt is calculated using a simple degree-day method ([[Gerten et al., 2004]]). The soil is parameterised as a bucket model. The status of soil moisture of the soil layers is updated daily, accounting for throughfall, snowmelt, evapotranspiration, percolation and runoff. Percolation rates for the soil layers depend on soil type and decline exponentially with soil moisture. Total runoff is calculated as water in excess of field capacity from the soil layers and water percolating through the second soil layer. The current version of LPJmL has no explicit representation of groundwater recharge, but a groundwater scheme is under development. The daily (subsurface) runoff includes the renewable fraction of groundwater, but without any time delay. | |||
All runoff is routed daily through a gridded river network, representing a system of rivers, natural lakes and reservoirs, using a simple routing algorithm ([[Rost et al., 2008]]). Local runoff is added to surface water storage in the cell, and subsequently flows downstream at a constant flow velocity of 1 m s-1 until reaching a lake or reservoir. Water accumulates in lakes and reservoirs, and outflow depends on actual storage relative to the maximum storage capacity (for lakes) and the operational purpose of the reservoir ([[Biemans et al., 2011]]). For man-made reservoirs, see further below ([[Biemans et al., 2011]]) | |||
===Supply and demand for irrigation water=== | |||
Water availability and demand in agriculture is simulated with LPJmL’s irrigation module and an algorithm to simulate the operation of large reservoirs to supply water to irrigated areas ([[Biemans et al., 2013]]). | |||
The irrigation demand module (Figure Flowchart) is described in detail by Rost et al. ([[Rost et al., 2008|2008]]). Crop net irrigation demand is defined as the minimum atmospheric evaporative demand and the amount of water needed to fill the soil to field capacity. The irrigation withdrawal demand – the gross demand –is higher than the net water demand due to losses through evaporation, interception and conveyance. Thus, the quantity of water demanded by crops (water consumption) is always less than the quantity withdrawn (water use). This gross demand is calculated as the product of the crop irrigation demand and an irrigation efficiency that depends on the irrigation system (sprinker, surface or drip) that is allocated per country, as well as local soil characteristics ([[Jägermeyr et al., 2015]]). | |||
Irrigation water is extracted from the rivers and lakes in the grid cell or a neighbouring grid cell. If these local surface water sources cannot meet the total demand, water is extracted from nearby reservoirs, if available. Finally, there is an option to supply from an unlimited source that can be interpreted as non-sustainable groundwater extraction or water imported from another basin. By excluding these water sources in a series of model runs, irrigation water supply and crop production can be attributed to different water sources. | |||
By | |||
===Large reservoirs=== | |||
Some 50% of global river systems are regulated by dams, most of which are in basins where there is irrigation and economic activity ([[Nilsson et al., 2005]]). The main purpose of approximately one-third of all large reservoirs is irrigation. Thus, in estimating agricultural water use, man-made reservoirs have to be taken into account. | |||
The reservoir operation module | The reservoir operation module in LPJmL ([[Biemans et al., 2011]]) distinguishes three types of reservoirs: reservoirs used primarily for irrigation; reservoirs used primarily for other purposes (e.g., hydropower and flood control) but also for irrigation; and reservoirs not used for irrigation. Each type of reservoir is managed differently. The outflow of irrigation reservoirs follows the temporal pattern of irrigation demand, whereas the other reservoirs are intended to release equal quantities of water throughout the year. Water from irrigation reservoirs is supplied to downstream irrigated areas. | ||
===Water demand in other sectors=== | ===Water demand in other sectors=== | ||
Water demands for electricity, industries and households are calculated in <nowiki>[[TIMER model version overview| TIMER]]</nowiki>, following the method developed in [[Bijl et al., 2016]]. All three demands are calculated in separate sub-models, and are the product of an activity level, the water intensity of that activity, and efficiency factors. Future demands are based on historical water use obtained from AQUASTAT, and for the industry sector partly on the WATERGAP model ([[Florke et al., 2013]]). For electricity, the cooling water demands depend on the waste heat of power plants, and therefore on the fuel and power plant type determined in the [[Energy supply]] module. It also depends on the cooling type and efficiency. | |||
Once-through cooling systems use large volumes of surface water that are returned almost entirely to the water body from which they were extracted, albeit at an elevated temperature. Wet cooling towers exploit the evaporation heat capacity of water and, thus require much lower water volumes. However, a significant part of the cooling water evaporates during the process and does not return to the original water body. In some regions, cooling ponds are used, where cooling water is pumped and recycled in a closed loop, with water demand somewhere between the once-through and wet tower cooling systems. Finally, dry cooling systems are deployed that use air as a coolant and thus do not require cooling water. The water demands are based on [[Macknick et al., 2011]], and transformed to water demand per unit of excess heat. Municipal and industrial water demands are functions of population size and Industry Value Added (IVA), respectively. They are influenced by GDP per capita and assumptions on efficiency improvements. | |||
All non-agricultural water demands are calculated at the regional scale on a yearly timestep and subsequently downscaled to 0.5x0.5 degree grid cells using spatial explicit population data. | |||
====Impact indicators=== | ===Water extractions=== | ||
Water stress is often presented as | Water requirements in other sectors are extracted from local surface water, if available (rather than from reservoirs). Meeting the demand from these sectors receives priority over water withdrawal for irrigation. | ||
</div>{{DisplayFigureTemplate|Baseline figure Water}} | |||
=== Environmental flow requirements === | |||
Environmental Flow Requirements (EFRs) are defined as the quantity, timing and quality of water flows required to sustain freshwater and estuarine ecosystems ([[IRF, 2007]]). While these are difficult to quantify on a global scale, not including them at all can lead to an overestimation of available resources. Several global studies have therefore applied a proxy value, through means of a minimum discharge requirement ([[Gerten et al., 2013]]; [[Richter et al., 2011]]; [[Pastor et al., 2019]]; [[Jägermeyr et al., 2017]]). In IMAGE, EFRs are implemented following the methodology as developed by [[Pastor et al., 2014]]. This method is based on maintaining a percentage of the ‘pristine’ flow, which is the discharge without recent (i.e., less than 50 years) land-use developments and without withdrawals for irrigation and other sectors. <div class="page_standard"> | |||
===Impact indicators=== | |||
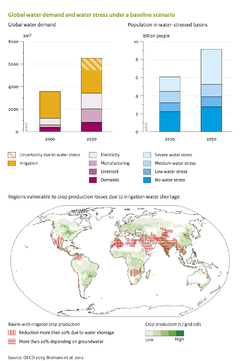
Water stress is often presented as the withdrawal-to-availability ratio at basin or country level. The population living with water stress is estimated by overlaying such a water-stress (or water availability) map with a population density map. These indicators are used to present IMAGE-LPJmL results (for instance, in the [[OECD Environmental Outlook to 2050 (2012) project|OECD Environmental Outlook]], see Figure) but they mask the potential occurrence of water shortages in the short-term or on sub-basin scale. Thus, water stress should also be calculated at higher spatial and temporal resolutions, as can principally be done with LPJmL (see [[Biemans, 2012]]). | |||
Other water related impacts that can be addressed with IMAGE are impacts of water shortage on yields, and the impact of climate on aridity (which is the ratio between rainfall and potential evapotranspiration). Impacts of efficiency improvements in irrigation and rainwater management can be analyzed through their effects on these indicators, see for example also [[Jägermeyr et al., 2017]]. | |||
</div> | |||
Latest revision as of 17:21, 19 November 2021
Parts of Water/Description
| Component is implemented in: |
|
| Related IMAGE components |
| Projects/Applications |
| Key publications |
| References |
Model description of Water
In IMAGE, the hydrological cycle is represented by LPJmL (Bondeau et al., 2007; Gerten et al., 2013; Schaphoff et al., 2018a), which simulates the global hydrological cycle as part of the dynamics of natural vegetation and agricultural production systems. Because LPJmL is linked to IMAGE, there is consistency in the way the carbon cycle, natural vegetation dynamics, crop growth and production, land-use allocation and the water balance are modelled.
Data on annual land cover and land use are used as input to LPJmL, including information on the location of irrigated areas and crop types (Figure Flowchart and Input/Output Table at Introduction part). This affects the amount of water that evaporates and runs off, as well as the amount of water needed for irrigated crops during the (simulated) growing season. Simultaneously, information on water availability and potential yields calculated by LPJmL is taken into account in the Land-use allocation model to identify suitable locations to expand irrigated areas. From the energy module, LPJmL receives water demands for industries, households and electricity. Together with water for irrigation these make up the total water demands in LPJmL.
Climate is used as input in LPJmL to determine potential evapotranspiration, and the precipitation input to the water balance (Gerten et al., 2004). The Crops and grass module, which is also part of LPJmL, calculates irrigation water demand based on crop characteristics, soil moisture and climate. If the amount of water available for irrigation is limited, water stress will occur which leads to reduction of crop yields calculated by the crop and grassland model.
The natural hydrological cycle
The Hydrology module in LPJmL consists of a vertical water balance (Gerten et al., 2004;Schaphoff et al., 2013) and a lateral flow component (Rost et al., 2008) that are simulated at 0.5 degree resolution in daily time steps (Figure Flowchart). The soil in each grid cell is represented by a five-layer soil column of 0.2, 0.3, 0.5, 1.0 and 1.0 m depth, partly covered with natural vegetation or crops.
The potential evapotranspiration rate in each grid cell depends primarily on net radiation and temperature, and is calculated using the Priestley-Taylor approach (Gerten et al., 2004). The actual evapotranspiration is calculated as the sum of three components: evaporation of water stored in the canopy (interception), bare soil evaporation and plant transpiration (Gerten et al., 2004). Water storage in the canopy is a function of vegetation type, leaf area index (LAI) and precipitation amount. Plant transpiration is modelled as the minimum of atmospheric demand and plant water supply. Plant water supply depends on the plant-dependent maximum transpiration rate and relative soil moisture. Soil evaporation occurs in the proportion of land in the grid cell that is not covered by vegetation. It equals potential evaporation when the soil moisture of the upper 20 cm is at field capacity, and declines linearly with relative soil moisture.
Precipitation reaching the soil (throughfall, precipitation minus interception) either accumulates as snow or infiltrates into the soil. Snowmelt is calculated using a simple degree-day method (Gerten et al., 2004). The soil is parameterised as a bucket model. The status of soil moisture of the soil layers is updated daily, accounting for throughfall, snowmelt, evapotranspiration, percolation and runoff. Percolation rates for the soil layers depend on soil type and decline exponentially with soil moisture. Total runoff is calculated as water in excess of field capacity from the soil layers and water percolating through the second soil layer. The current version of LPJmL has no explicit representation of groundwater recharge, but a groundwater scheme is under development. The daily (subsurface) runoff includes the renewable fraction of groundwater, but without any time delay.
All runoff is routed daily through a gridded river network, representing a system of rivers, natural lakes and reservoirs, using a simple routing algorithm (Rost et al., 2008). Local runoff is added to surface water storage in the cell, and subsequently flows downstream at a constant flow velocity of 1 m s-1 until reaching a lake or reservoir. Water accumulates in lakes and reservoirs, and outflow depends on actual storage relative to the maximum storage capacity (for lakes) and the operational purpose of the reservoir (Biemans et al., 2011). For man-made reservoirs, see further below (Biemans et al., 2011)
Supply and demand for irrigation water
Water availability and demand in agriculture is simulated with LPJmL’s irrigation module and an algorithm to simulate the operation of large reservoirs to supply water to irrigated areas (Biemans et al., 2013).
The irrigation demand module (Figure Flowchart) is described in detail by Rost et al. (2008). Crop net irrigation demand is defined as the minimum atmospheric evaporative demand and the amount of water needed to fill the soil to field capacity. The irrigation withdrawal demand – the gross demand –is higher than the net water demand due to losses through evaporation, interception and conveyance. Thus, the quantity of water demanded by crops (water consumption) is always less than the quantity withdrawn (water use). This gross demand is calculated as the product of the crop irrigation demand and an irrigation efficiency that depends on the irrigation system (sprinker, surface or drip) that is allocated per country, as well as local soil characteristics (Jägermeyr et al., 2015).
Irrigation water is extracted from the rivers and lakes in the grid cell or a neighbouring grid cell. If these local surface water sources cannot meet the total demand, water is extracted from nearby reservoirs, if available. Finally, there is an option to supply from an unlimited source that can be interpreted as non-sustainable groundwater extraction or water imported from another basin. By excluding these water sources in a series of model runs, irrigation water supply and crop production can be attributed to different water sources.
Large reservoirs
Some 50% of global river systems are regulated by dams, most of which are in basins where there is irrigation and economic activity (Nilsson et al., 2005). The main purpose of approximately one-third of all large reservoirs is irrigation. Thus, in estimating agricultural water use, man-made reservoirs have to be taken into account. The reservoir operation module in LPJmL (Biemans et al., 2011) distinguishes three types of reservoirs: reservoirs used primarily for irrigation; reservoirs used primarily for other purposes (e.g., hydropower and flood control) but also for irrigation; and reservoirs not used for irrigation. Each type of reservoir is managed differently. The outflow of irrigation reservoirs follows the temporal pattern of irrigation demand, whereas the other reservoirs are intended to release equal quantities of water throughout the year. Water from irrigation reservoirs is supplied to downstream irrigated areas.
Water demand in other sectors
Water demands for electricity, industries and households are calculated in [[TIMER model version overview| TIMER]], following the method developed in Bijl et al., 2016. All three demands are calculated in separate sub-models, and are the product of an activity level, the water intensity of that activity, and efficiency factors. Future demands are based on historical water use obtained from AQUASTAT, and for the industry sector partly on the WATERGAP model (Florke et al., 2013). For electricity, the cooling water demands depend on the waste heat of power plants, and therefore on the fuel and power plant type determined in the Energy supply module. It also depends on the cooling type and efficiency.
Once-through cooling systems use large volumes of surface water that are returned almost entirely to the water body from which they were extracted, albeit at an elevated temperature. Wet cooling towers exploit the evaporation heat capacity of water and, thus require much lower water volumes. However, a significant part of the cooling water evaporates during the process and does not return to the original water body. In some regions, cooling ponds are used, where cooling water is pumped and recycled in a closed loop, with water demand somewhere between the once-through and wet tower cooling systems. Finally, dry cooling systems are deployed that use air as a coolant and thus do not require cooling water. The water demands are based on Macknick et al., 2011, and transformed to water demand per unit of excess heat. Municipal and industrial water demands are functions of population size and Industry Value Added (IVA), respectively. They are influenced by GDP per capita and assumptions on efficiency improvements.
All non-agricultural water demands are calculated at the regional scale on a yearly timestep and subsequently downscaled to 0.5x0.5 degree grid cells using spatial explicit population data.
Water extractions
Water requirements in other sectors are extracted from local surface water, if available (rather than from reservoirs). Meeting the demand from these sectors receives priority over water withdrawal for irrigation.
Environmental flow requirements
Environmental Flow Requirements (EFRs) are defined as the quantity, timing and quality of water flows required to sustain freshwater and estuarine ecosystems (IRF, 2007). While these are difficult to quantify on a global scale, not including them at all can lead to an overestimation of available resources. Several global studies have therefore applied a proxy value, through means of a minimum discharge requirement (Gerten et al., 2013; Richter et al., 2011; Pastor et al., 2019; Jägermeyr et al., 2017). In IMAGE, EFRs are implemented following the methodology as developed by Pastor et al., 2014. This method is based on maintaining a percentage of the ‘pristine’ flow, which is the discharge without recent (i.e., less than 50 years) land-use developments and without withdrawals for irrigation and other sectors.
Impact indicators
Water stress is often presented as the withdrawal-to-availability ratio at basin or country level. The population living with water stress is estimated by overlaying such a water-stress (or water availability) map with a population density map. These indicators are used to present IMAGE-LPJmL results (for instance, in the OECD Environmental Outlook, see Figure) but they mask the potential occurrence of water shortages in the short-term or on sub-basin scale. Thus, water stress should also be calculated at higher spatial and temporal resolutions, as can principally be done with LPJmL (see Biemans, 2012).
Other water related impacts that can be addressed with IMAGE are impacts of water shortage on yields, and the impact of climate on aridity (which is the ratio between rainfall and potential evapotranspiration). Impacts of efficiency improvements in irrigation and rainwater management can be analyzed through their effects on these indicators, see for example also Jägermeyr et al., 2017.