Energy conversion/Description: Difference between revisions

From IMAGE
Jump to navigation Jump to search
No edit summary
(Added hydrogen sector improvements)
 
(96 intermediate revisions by 9 users not shown)
Line 1: Line 1:
{{ComponentSubDescriptionTemplate
{{ComponentDescriptionTemplate
|Flowchart=FlowDiagramElectrictyModel.png
|Reference=Hoogwijk, 2004; Van Vuuren, 2007; Hendriks et al., 2004b; Van Ruijven et al., 2007; Ueckerdt et al., 2016; Gernaat et al., 2014; Köberle et al., 2015; De Boer and Van Vuuren, 2017;
|AltText=Flow diagram for the electricity model in TIMER
}}
|CaptionText=Flow diagram for the electricity model in TIMER
<div class="page_standard">
|Description=<h2>Electric power model</h2>
 
In our description, we concentrate on the most complex model first. Next, we indicate how the hydrogen model is derived from this. The figure on the right shows the electricity model. The main assumptions, inputs and outputs of the module are shown as well as the route from inputs to outputs. It illustrates the diversity of technologies that can be used to produce electricity as well as the two stages for arriving at the output demand for primary energy carriers – the investment strategy and the operational strategy.
[[TIMER model|TIMER]] includes two main energy conversion modules: Electric power generation and hydrogen generation. Below, electric power generation is described in detail. In addition, the key characteristics of the hydrogen generation model, which follows a similar structure, are presented.
===Total demand for new capacity===  
 
Investment decisions in the electricity model are made in response to expected electricity demand and to changes in relative generation costs (see also Hoogwijk, 2004). The demand for capacity is derived from the forecast for the simultaneous maximum demand plus a reserve margin of about 10%. A challenge in the simulation of electricity production in an aggregated integrated assessment model is that in reality, often much more detailed consideration play a role. Our model uses a simplified approach in which the simultaneous maximum demand is calculated on the basis of the gross electricity demand: net electricity demand plus electricity trade and transmission losses. The model determines a monthly load duration curve for each region. The form of the Load Duration Curve has been preset by expected changes in region-specific factors such as heating and cooling degree days, daylight and assumed patterns of appliance use. In general, this results in a monthly variation with a maximum value of 20-30% above the average value and a minimum value 40% below the average value. The demand for new capacity equals the difference between required capacity and existing capacity, plus replacement of plants at the end of their life (the lifetime of plants varies, depending on the technology, from 30 to 50 years).
===Electric power generation===
In TIMER, electricity can be generated by 32 technologies. These include the VRE sources solar utility scale photovoltaic (PV), residential photovoltaics (RPV), concentrated solar power (CSP), ocean wave power and onshore and offshore wind power. Other technology types are natural gas-, coal-, biomass- and oil-fired power plants. These power plants come in multiple variations: conventional, combined cycle, carbon capture and storage (CCS) and combined heat and power (CHP). The electricity sector in TIMER also describes the use of nuclear, other renewables (mainly geothermal power) and hydroelectric power. A recent addition is the use of hydrogen for electricity and heat generation. ([[De Boer and Van Vuuren, 2017]])


===Decisions to invest in specific options===
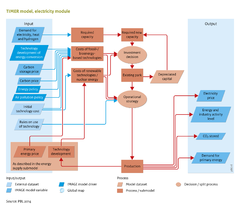
As shown in the [[Flowchart Energy conversion|flowchart]], two key elements of the electric power generation are the investment strategy and the operational strategy in the sector. A challenge in simulating electricity production in an aggregated model is that in reality electricity production depends on a range of complex factors, related to costs, reliance, and technology ramp rates. Modelling these factors requires a high level of detail and thus IAMs, such as TIMER, concentrate on introducing a set of simplified, meta relationships ([[Hoogwijk, 2004]]; [[Van Vuuren, 2007]]; [[De Boer and Van Vuuren, 2017]]).
Next, a decision is made to invest in different technologies on the basis of their total costs. For this a multinomial logit equation is used, assigning the largest market share to the lowest costs options. The cost of each plant is broken down into a number of categories: i.e. investment costs, fuel costs, operational and maintenance costs and other costs (see further). Notably, an exception is made for hydropower. The capacity for hydropower is exogenously prescribed, given the fact that in the construction of large hydropower plants often other considerations than electricity production (for instance flood control) play a role. In the equations, some exceptions are added to account for limitations in supply (e.g. restriction in bio-mass availability).  


INV =INVTOT *  (LCOE+PREF)<sup>-labda</sup>/SIGMA(LCOE+PREF)<sup>-labda</sup>
====Total demand for new capacity====
<div class="version changev31">
The electricity generation capacity required to meet the demand per region is based on a forecast of the maximum annual electricity demand plus a reserve margin. The reserve margin consists of a general reserve margin of 10-20% on peak demand plus a compensation for imperfect capacity credits (the reliability of a plant type to supply power during the peak hours) of existing capacity. The maximum annual demand is calculated on the basis of an assumed shape of the load duration curve (LDC) and the gross electricity demand. The latter comprises the net electricity demand from the end-use sectors plus electricity trade and transmission losses. An LDC shows the distribution of load over a certain timespan in a downward form. The peak load is plotted to the left of the LDC and the lowest load is plotted to the right. The shape of the LDC is based on work by Ueckerdt et al. ([[Ueckerdt et al., 2016|2016]]), who derived regional normalized residual LDCs (RLDC) for different solar and wind shares, including the application of optimized electricity storage.


With investments equal to the new investments into specific technology i, LCOE the levelized costs of electricity generation of technology i, preference the additional costs assigned to technology i based on preferences and labda the logit parameter determining the sensitivity to price differences.
The final demand for new generation capacity is equal to the difference between the required and existing capacity. Power capacity is assumed to be replaced at the end of its lifetime, which varies from 25 to 80 years, depending on the technology.


===Operational strategy===
Capacity can also be decommissioned before the end of the technical lifetime. This so-called early retirement can occur if the operation of the capacity has become relatively expensive compared to the operation and construction of new capacity. The operational costs include fixed O&M, variable O&M, fuel and CCS costs. Capacity will not be retired early if the capacity has a backup role, characterized by a low load factor resulting in low operational costs and carbon emissions. ([[De Boer and Van Vuuren, 2017]])
For the operational strategy, power plants are basically used based on operational costs (the lowest costs options are used most). This implies that capital-intensive plants with low operational costs, such as renewables and nuclear energy, will therefore in principle operate as many hours as possible. To some degree this is also true for other plants with low operational costs (e.g. coal). Therefore, the operational decision is represented by the following steps:
</div>
# first intermittent renewable sources (PV and wind) are assigned, followed by hydropower as these options have the lowest operational costs;
# in the next step, the peak load capacity is assigned on the basis of operational costs and the ability of options to function as peak load capacity.
# In the final step, base load is assigned on the basis of the remaining capacity, operational costs and the ability of options to function as base load capacity.;


In reality, the merit order strategy is more complex, given the many additional requirements that exist with respect to reliability and start-up times.  
====Decisions to invest in specific options ====
In the model, the decision to invest in generation technologies is based on the levelized cost of electricity (LCOE; in USD/kWhe) produced per technology, using a multinomial logit equation that assigns larger market shares to the lower cost options.


===Fossil fuel and bio-energy of power plants===
An important variable used in determining the LCOE is the expected amount of electricity generated. Often, the LCOEs of technologies are compared at maximum full load hours. However, only a limited share of the installed capacity will actually generate electricity at full load. This effect is captured in a heuristic: different load bands have been introduced to link the investment decision to expected dispatch. The different load bands are distributed among the LDC, resulting in a load factor for each load band. The inclusion of different load factors for each load band means that less capital-intensive technologies are attractive to use for lower load factor load bands. These are likely to be gas-fired peaker plants. For load bands with higher load factors, the electricity submodule chooses technologies with lower operational costs. These are likely to be base load plants, such as coal-fired or nuclear power plants. VRE load factors per load band are derived from the marginal load band contributions resulting from the RLDC. A system with more VRE sources will result in lower residual load factors and therefore in a higher demand for peak or mid load technologies. ([[De Boer and Van Vuuren, 2017]])
A total of 20 different plant types generating electricity from fossil fuels and bio-energy are modeled (in additional to PV, wind, hydro and nuclear power). These plant types represent different combinations of
# conventional technology;
# gasification and combined cycle technology;
# combined-heat-and-power and,
# carbon-capture and storage (see also Hendriks et al., 2004). The efficiency and capital requirement of these plant types are determined by exogenous assumptions that describe technological progress of typical components of these plants (the characteristics of the total set are derived from these typical components).  
* For conventional plants, the coal-based plant is defined in terms of overall efficiency and investment costs, which are broken down into fuel handling, plant and fuel gas cleaning and operational costs. The requirements for all other conventional plants (oil, natural gas and bio-energy) are derived by indicating differences for investments for a) desulphurization, b) fuel handling and c) efficiency.
* For Combined Cycle plants, the natural gas combined cycle plant is set as standard. Other plants are defined by indicating additional capital costs for gasification, efficiency losses due to gasification and operation and maintenance (O & M) costs for fuel handling.  
* Carbon capture and storage plants are assumed to be Combined Cycle plants with corrections (as a function of the carbon content of the fuel) for efficiency, investment costs, O&M costs (for capture) and storage costs.
* CHP plants can be based on Combined Cycle plants or on conventional plants (the model selects the lowest cost option). In both cases a small increase in capital costs is assumed in combination with a lower efficiency for electric conversion and an added factor for heat efficiency (in other words, the model only includes large-scale CHP).


The total costs of these plants are:
The standard costs of each option can be broken down into several categories: investment or capital cost; fuel cost; fixed and variable operational and maintenance costs; construction costs; and carbon capture and storage costs.
LCOE = 1/ LoadFactor* Cap * Ann + OM + 1/Eff * (FuelCost + CO2Emis* StorCost) * kWhtoGJ
* The capital costs of power generating technologies can be exogenously described, but they can also develop as a result of endogenous learning mechanisms explained [[Technical learning|here]]. For the endogenous method, technologies are split up in different cost components. These components have individual learning characteristics, like learning rate, floor costs and start costs. However, spillovers are possible between technologies and regions. Technology spillovers occur when technologies share a component.
* Fuel cost result from the supply modules described [[Energy supply|here]].
* Fixed and variable operation and maintenance costs develop according to the same principles as the capital costs
* Construction costs result from interest paid during construction. Construction times vary among the technologies.
* More information on carbon capture and storage cost can be found [[Carbon capture and storage|here]].
Also, additional costs are distinguished: backup costs; curtailment costs; VRE load factor decline; storage costs; and transmission and distribution costs.
* Backup costs have been added to represent the additional costs required in order to meet the capacity and energy production requirements of a load band. Backup costs are usually higher for technologies with low capacity credits. Backup costs include all standard cost components for the chosen backup technology. This backup capacity is installed together with regular investments in load bands
* Curtailment costs are only relevant for VRE technologies and CHP. Curtailments occur when the supply exceeds the demand. The degree to which curtailment occurs depends on VRE share, storage use and the regional correlation between electricity demand and VRE or CHP supply. Curtailment influences the LCOE by reducing the potential amount of electricity that could be generated.
* Load factor reduction results from the utilisation of resource sites with less favourable environmental conditions, such as lower wind speeds, lower water discharge or less solar irradiation. This results in a lower potential load influencing the LCOE by reducing the potential electricity generation. The development of load factor reduction is captured in cost supply curves. For more information on the TIMER cost supply curves see: Hoogwijk ([[Hoogwijk, 2004|2004]]), Gernaat et al., ([[Gernaat et al., 2014|2014]]), Koberle et al., ([[Köberle et al., 2015|2015]]) and Gernaat et al., (<nowiki>[[2018]]</nowiki>)
* Storage use has been optimised in the RLDC data set. For more information on storage use, see Ueckerdt et al. (n.d.).
* Transmission and distribution costs are simulated by adding a fixed relationship between the amount of capacity and the required amount of transmission and distribution capital. VRE cost supply curves contain additional transmission costs resulting from distance between VRE potential and demand centres.


Renewable energy.  
The exceptions are ''other renewables'' and CHP. ''Other renewables'' are exogenously prescribed, because of a lack of available data. The demand for CHP capacity is heat demand driven. ([[De Boer and Van Vuuren, 2017]])
Apart from fossil-fuel and bio-energy fired plants, the model distinguishes hydropower, solar power, wind power and nuclear power. The costs of technologies are described in terms of learning and depletion dynamics.


LCOE = 1/ LoadFactor* (Cap*Ann * Depl * LearnFactor) + OM + SystemIntegration
Finally, in the equations, some constraints are added to account for limitations in supply, for example restrictions on biomass availability. For a more detailed description on electricity sector investments in TIMER, see [[De Boer and Van Vuuren, 2017]]).


For renewable energy sources with an intermittent character (wind and solar power), additional costs are borne for discarded electricity (if production exceeds demand), back-up capacity, additional required spinning reserve (the two last ones to avoid loss of power if supply of wind or solar power suddenly drops; spinning reserve is formed by power stations operating below maximum capacity, which can be scaled up in a relatively short time) and depletion (see also Hoogwijk, 2004).
====Operational strategy====
* To determine discarded electricity for each load fraction a comparison is made between supply and demand. It is assumed that wind power can be either fully in phase or fully out-of-phase with electricity demand: both situations are calculated and the average is used. For PV, it is assumed that supply mainly occurs during the hours at which demand is highest. If supply exceeds demand (calculated for each individual month based on available data on monthly variation in supply), the electricity produced is assumed to be discarded, reducing the effective load factor of wind and solar electricity (and thus increasing their costs).
* Depletion is modeled as a function of built-capacity. The costs decrease via the depletion factor. The underlying assumptions are described in the supply chapter.
* Back-up capacity is added to account for the low capacity credit (meaning the contribution of a plant to a reliable supply of electricity at any moment in time) of the intermittent sources. For the first 5% penetration of the intermittent capacity, the capacity credit equals the load factor of the wind turbines. If the penetration of intermittent sources increases further, the capacity credit decreases. The costs of back-up power (for which capacity with a high capacity credit but low capital costs is used) are allocated to the intermittent source (system integration factor).
* The required spinning reserve is assumed to be 3.5% of the installed capacity of the conventional park. If wind and solar photo-voltaic cells (PV) penetrate the market, the additional required spinning reserve equals 15% of the intermittent capacity, but only after the existing 3.5% in exceeded. These costs are allocated to the intermittent source (system integration factor).


===Nuclear power===
The demand for electricity is met by the installed capacity of power plants. The available capacity is used according to the merit order of the different types of plants; technologies with the lowest variable costs are dispatched first, followed by other technologies based on an ascending order of variable costs. This results in a cost-optimal dispatch of technologies. The dispatch of VRE is described by the RLDC dataset. CHP dispatch is distributed based on monthly heating degree days. Within each month, the CHP load stays constant. Hydropower has a monthly dispatch potential. This limited availability of hydropower is distributed so that so that it creates most system benefits. Generally, this has a peak shaving effect on residual demand for electricity.
The costs equation of nuclear power is a combination of that the of the fossil fuel and renewable energy plants:
LCOE = 1/ LoadFactor* (Cap*Ann * LearnFactor) + OM + 1/Eff * (FuelCost) * kWhtoGJ


Similar to the renewable options, learning for nuclear power is prescribed via learning curves. For nuclear power, depletion, however, occurs via increasing fuel costs. The fuel costs are determined on the basis of depletion uranium and thorium resources (as described in the chapter on energy resources).
===Hydrogen generation===
The structure of the hydrogen generation submodule is similar to that for electric power generation ([[Van Ruijven et al., 2007]]) but with following differences:
#There are 17 supply options for hydrogen production:
#* coal, oil, natural gas and bioenergy, with and without carbon capture and storage (8 plants);
#* grid electrolysis:
#** a technology producing hydrogen at a constant rate resulting in a baseload electricity demand
#** a technology producing hydrogen just from cheap VRE curtailments, reducing curtailment levels in the electricity sector
#*direct renewable electrolysis:
#** combining solar PV, CSP, onshore wind and offshore wind technologies directly with an electrolyser
#** avoids electricity grid costs
#** shared technological learning with electricity production technologies 
#* small scale technologies at low hydrogen demand levels:
#** small methane reform plant
#** small scale electrolyser
#No description of preferences for different power plants is taken into account in the operational strategy. The load factor for each option equals the total production divided by the capacity for each region. The direct electrolysis technologies and the curtailment electrolyser are exceptions: here the load factor is limited by the supply technology
#Intermittence does not play an important role because hydrogen can be stored to some degree. Thus, there are no equations simulating system integration.
#Hydrogen can be traded. A trade model is added, similar to those for fossil fuels described in [[Energy supply]].


===Hydrogen===
See the additional info on [[Grid and infrastructure]].
The hydrogen model follows a similar structure as the electric power model. There are, however, some important differences:
</div>
* In total, the hydrogen model distinguishes between 11 supply options: 1-4) H2 production plants on the basis of coal, oil, natural gas and bio-energy, 5-8) Similar to 2-5 but in combination with CCS, 9) Bio-energy production from electrolysis, 10) direct bio-energy production from solar thermal processes and 11) 1) Small methane reform plants.  
* For simplification, no description of preferences for different power plants is accounted for in the operational strategy. In other words, the load factor for each option equals the total production divided by the capacity for each region.
* Hydrogen can be traded. Therefore, a trade model is added, similar to the fuel trade models for fossil fuels (See Chapter on Resources).
* Intermittency does not play an important role as hydrogen can be stored to some degree. Therefore there are no equations simulation the role of system integration included.
|Status=Publishable
}}

Latest revision as of 11:37, 3 November 2022

Link to framework components overview

Parts of Energy conversion/Description

  1. Introduction page
  2. Model description
  3. Policy issues
  4. Data, uncertainty and limitations
  5. Overview of references
    6. Additional info
  6. Carbon capture and storage
  7. Grid and infrastructure
  8. Technical learning
Component is implemented in:
Aggregated component:Components:
Related IMAGE components
Projects/Applications
Models/Databases
Key publications
References
TIMER model, electricity module
Flowchart Energy conversion. See also the Input/Output Table on the introduction page.

Model description of Energy conversion

TIMER includes two main energy conversion modules: Electric power generation and hydrogen generation. Below, electric power generation is described in detail. In addition, the key characteristics of the hydrogen generation model, which follows a similar structure, are presented.

Electric power generation

In TIMER, electricity can be generated by 32 technologies. These include the VRE sources solar utility scale photovoltaic (PV), residential photovoltaics (RPV), concentrated solar power (CSP), ocean wave power and onshore and offshore wind power. Other technology types are natural gas-, coal-, biomass- and oil-fired power plants. These power plants come in multiple variations: conventional, combined cycle, carbon capture and storage (CCS) and combined heat and power (CHP). The electricity sector in TIMER also describes the use of nuclear, other renewables (mainly geothermal power) and hydroelectric power. A recent addition is the use of hydrogen for electricity and heat generation. (De Boer and Van Vuuren, 2017)

As shown in the flowchart, two key elements of the electric power generation are the investment strategy and the operational strategy in the sector. A challenge in simulating electricity production in an aggregated model is that in reality electricity production depends on a range of complex factors, related to costs, reliance, and technology ramp rates. Modelling these factors requires a high level of detail and thus IAMs, such as TIMER, concentrate on introducing a set of simplified, meta relationships (Hoogwijk, 2004; Van Vuuren, 2007; De Boer and Van Vuuren, 2017).

Total demand for new capacity

The electricity generation capacity required to meet the demand per region is based on a forecast of the maximum annual electricity demand plus a reserve margin. The reserve margin consists of a general reserve margin of 10-20% on peak demand plus a compensation for imperfect capacity credits (the reliability of a plant type to supply power during the peak hours) of existing capacity. The maximum annual demand is calculated on the basis of an assumed shape of the load duration curve (LDC) and the gross electricity demand. The latter comprises the net electricity demand from the end-use sectors plus electricity trade and transmission losses. An LDC shows the distribution of load over a certain timespan in a downward form. The peak load is plotted to the left of the LDC and the lowest load is plotted to the right. The shape of the LDC is based on work by Ueckerdt et al. (2016), who derived regional normalized residual LDCs (RLDC) for different solar and wind shares, including the application of optimized electricity storage.

The final demand for new generation capacity is equal to the difference between the required and existing capacity. Power capacity is assumed to be replaced at the end of its lifetime, which varies from 25 to 80 years, depending on the technology.

Capacity can also be decommissioned before the end of the technical lifetime. This so-called early retirement can occur if the operation of the capacity has become relatively expensive compared to the operation and construction of new capacity. The operational costs include fixed O&M, variable O&M, fuel and CCS costs. Capacity will not be retired early if the capacity has a backup role, characterized by a low load factor resulting in low operational costs and carbon emissions. (De Boer and Van Vuuren, 2017)

Decisions to invest in specific options

In the model, the decision to invest in generation technologies is based on the levelized cost of electricity (LCOE; in USD/kWhe) produced per technology, using a multinomial logit equation that assigns larger market shares to the lower cost options.

An important variable used in determining the LCOE is the expected amount of electricity generated. Often, the LCOEs of technologies are compared at maximum full load hours. However, only a limited share of the installed capacity will actually generate electricity at full load. This effect is captured in a heuristic: different load bands have been introduced to link the investment decision to expected dispatch. The different load bands are distributed among the LDC, resulting in a load factor for each load band. The inclusion of different load factors for each load band means that less capital-intensive technologies are attractive to use for lower load factor load bands. These are likely to be gas-fired peaker plants. For load bands with higher load factors, the electricity submodule chooses technologies with lower operational costs. These are likely to be base load plants, such as coal-fired or nuclear power plants. VRE load factors per load band are derived from the marginal load band contributions resulting from the RLDC. A system with more VRE sources will result in lower residual load factors and therefore in a higher demand for peak or mid load technologies. (De Boer and Van Vuuren, 2017)

The standard costs of each option can be broken down into several categories: investment or capital cost; fuel cost; fixed and variable operational and maintenance costs; construction costs; and carbon capture and storage costs.

  • The capital costs of power generating technologies can be exogenously described, but they can also develop as a result of endogenous learning mechanisms explained here. For the endogenous method, technologies are split up in different cost components. These components have individual learning characteristics, like learning rate, floor costs and start costs. However, spillovers are possible between technologies and regions. Technology spillovers occur when technologies share a component.
  • Fuel cost result from the supply modules described here.
  • Fixed and variable operation and maintenance costs develop according to the same principles as the capital costs
  • Construction costs result from interest paid during construction. Construction times vary among the technologies.
  • More information on carbon capture and storage cost can be found here.

Also, additional costs are distinguished: backup costs; curtailment costs; VRE load factor decline; storage costs; and transmission and distribution costs.

  • Backup costs have been added to represent the additional costs required in order to meet the capacity and energy production requirements of a load band. Backup costs are usually higher for technologies with low capacity credits. Backup costs include all standard cost components for the chosen backup technology. This backup capacity is installed together with regular investments in load bands
  • Curtailment costs are only relevant for VRE technologies and CHP. Curtailments occur when the supply exceeds the demand. The degree to which curtailment occurs depends on VRE share, storage use and the regional correlation between electricity demand and VRE or CHP supply. Curtailment influences the LCOE by reducing the potential amount of electricity that could be generated.
  • Load factor reduction results from the utilisation of resource sites with less favourable environmental conditions, such as lower wind speeds, lower water discharge or less solar irradiation. This results in a lower potential load influencing the LCOE by reducing the potential electricity generation. The development of load factor reduction is captured in cost supply curves. For more information on the TIMER cost supply curves see: Hoogwijk (2004), Gernaat et al., (2014), Koberle et al., (2015) and Gernaat et al., ([[2018]])
  • Storage use has been optimised in the RLDC data set. For more information on storage use, see Ueckerdt et al. (n.d.).
  • Transmission and distribution costs are simulated by adding a fixed relationship between the amount of capacity and the required amount of transmission and distribution capital. VRE cost supply curves contain additional transmission costs resulting from distance between VRE potential and demand centres.

The exceptions are other renewables and CHP. Other renewables are exogenously prescribed, because of a lack of available data. The demand for CHP capacity is heat demand driven. (De Boer and Van Vuuren, 2017)

Finally, in the equations, some constraints are added to account for limitations in supply, for example restrictions on biomass availability. For a more detailed description on electricity sector investments in TIMER, see De Boer and Van Vuuren, 2017).

Operational strategy

The demand for electricity is met by the installed capacity of power plants. The available capacity is used according to the merit order of the different types of plants; technologies with the lowest variable costs are dispatched first, followed by other technologies based on an ascending order of variable costs. This results in a cost-optimal dispatch of technologies. The dispatch of VRE is described by the RLDC dataset. CHP dispatch is distributed based on monthly heating degree days. Within each month, the CHP load stays constant. Hydropower has a monthly dispatch potential. This limited availability of hydropower is distributed so that so that it creates most system benefits. Generally, this has a peak shaving effect on residual demand for electricity.

Hydrogen generation

The structure of the hydrogen generation submodule is similar to that for electric power generation (Van Ruijven et al., 2007) but with following differences:

  1. There are 17 supply options for hydrogen production:
    • coal, oil, natural gas and bioenergy, with and without carbon capture and storage (8 plants);
    • grid electrolysis:
      • a technology producing hydrogen at a constant rate resulting in a baseload electricity demand
      • a technology producing hydrogen just from cheap VRE curtailments, reducing curtailment levels in the electricity sector
    • direct renewable electrolysis:
      • combining solar PV, CSP, onshore wind and offshore wind technologies directly with an electrolyser
      • avoids electricity grid costs
      • shared technological learning with electricity production technologies
    • small scale technologies at low hydrogen demand levels:
      • small methane reform plant
      • small scale electrolyser
  2. No description of preferences for different power plants is taken into account in the operational strategy. The load factor for each option equals the total production divided by the capacity for each region. The direct electrolysis technologies and the curtailment electrolyser are exceptions: here the load factor is limited by the supply technology
  3. Intermittence does not play an important role because hydrogen can be stored to some degree. Thus, there are no equations simulating system integration.
  4. Hydrogen can be traded. A trade model is added, similar to those for fossil fuels described in Energy supply.

See the additional info on Grid and infrastructure.

Retrieved from "https://models.pbl.nl/index.php?title=Energy_conversion/Description&oldid=37012"