Energy conversion/Description: Difference between revisions
No edit summary |
No edit summary |
||
| Line 4: | Line 4: | ||
==Electric power generation== | ==Electric power generation== | ||
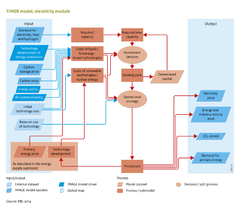
As shown in the flowchart, two key elements of the electric power generation are the investment strategy and the operational strategy in the sector. A challenge in simulating electricity production in an aggregated model is that in reality electricity production depends on a range of complex factors, related to costs, reliance, and the time required to switch on technologies. Modelling these factors requires a high level of detail and thus {{AbbrTemplate|IAM}}s such as [[TIMER model|TIMER]] concentrate on introducing a set of simplified, meta relationships ([[Hoogwijk, 2004]]; [[Van Vuuren, 2007]]). | As shown in the flowchart, two key elements of the electric power generation are the investment strategy and the operational strategy in the sector. A challenge in simulating electricity production in an aggregated model is that in reality electricity production depends on a range of complex factors, related to costs, reliance, and the time required to switch on technologies. Modelling these factors requires a high level of detail and thus ({{AbbrTemplate|IAM}}s) such as [[TIMER model|TIMER]] concentrate on introducing a set of simplified, meta relationships ([[Hoogwijk, 2004]]; [[Van Vuuren, 2007]]). | ||
===Total demand for new capacity=== | ===Total demand for new capacity=== | ||
Revision as of 17:09, 8 May 2014
Parts of Energy conversion/Description
| Component is implemented in: |
|
| Related IMAGE components |
| Projects/Applications |
| Models/Databases |
| Key publications |
| References |
Model description of Energy conversion
s such as TIMER concentrate on introducing a set of simplified, meta relationships (Hoogwijk, 2004; Van Vuuren, 2007).
Total demand for new capacity
The electricity capacity required to meet the demand per region is based on a forecast of the maximum electricity demand plus a reserve margin of about 10% (including the capacity credit assigned to different forms of electricity generation). Maximum demand is calculated on the basis of an assumed monthly shape of the load duration curve (LDC) and the gross electricity demand. The latter comprises the net electricity demand from the end-use sectors plus electricity trade and transmission losses (LDC) accounts for characteristics such as cooling and lighting demand). The demand for new generation capacity is the difference between the required and existing capacity. Power plants are assumed to be replaced at the end of their lifetime, which varies from 30 to 50 years, depending on the technology and is currently fixed in the model.
Decisions to invest in specific options
In the following step, a decision is made to invest in different generation technologies. In the model, this is done on the basis of the price of electricity (in USD/kWhe produced per technology, using a multinomial logit equation that assigns larger market shares to the lower cost options. The specific costs of each option is broken down into a number of categories: investment or capital costs (USD/kWe), fuel costs (USD/GJ), operational and maintenance costs (OM) and other costs (see further). An exception is hydropower capacity, which is exogenously prescribed, because large hydropower plants often have functions other than only electricity production (e.g. water supply and flood control). In the equations, some constraints are added to account for limitations in supply (e.g. restrictions on biomass availability). The investments needed for each option are given in the form of total investment in new generation capacity and the share of each individual technology (determined on the basis of price and preference).
Operational strategy
Use of power plants is based on operational costs, with low-cost technologies assumed to be used most often. This implies that capital-intensive plants with low operational costs, such as renewable and nuclear energy, operate as many hours as possible. To some degree, this is also true for other plants with low operational costs, such as coal. The operational decision is presented in the following three steps:
- Renewable sources PV and wind are assigned, followed by hydropower, because these options have the lowest operational costs;
- The peak load capacity (period of high electricity demand) is assigned on the basis of the operational costs of each available plant and the ability of these plants to provide peak load capacity;
- Base load (period of medium to low energy demand) is assigned on the basis of the remaining capacity (after steps 1 and 2), operational costs and the ability of options to provide the base load capacity.
Fossil-fuel and bio-energy power plants
A total of 20 types of power plants generating electricity using fossil fuels and bioenergy are included. These power plants represent different combinations of conventional technology, such as gasification and combined cycle (CC) technology; combined heat and power (CHP); and carbon capture and storage (CCS;(Hendriks et al., 2004b). The specific capital costs and thermal efficiencies of these types of plants are determined by exogenous assumptions that describe the technological progress of typical components of these plants:
- For conventional power plants, the coal-fired plant is defined in terms of overall efficiency and investment cost. The characteristics of all other conventional plants (using oil, natural gas or bioenergy) are described in the investment differences for desulphurisation, fuel handling and efficiency.
- For Combined Cycle (CC) power plants, the characteristics of a natural gas fired plant are set as the standard. Other CC plants (fuelled by oil, bioenergy and coal after gasification) are defined by indicating additional capital costs for gasification, efficiency losses due to gasification, and operation and maintenance (O&M) costs for fuel handling.
- Power plants with carbon-capture-and-storage systems (CCS) are assumed to be CC plants, but with fuel-specific lower efficiency and higher investment and O&M costs (related to capture and storage).
- The characteristics of combined-heat-and-power plants (CHP) are similar to those of other plants, but with an assumed small increase in capital costs, in combination with a lower efficiency for electric conversion and an added factor for heat efficiency.
The cost of one unit electricity generated is equal to the sum of the capital cost, operational and maintenance costs (O&M), fuel cost, and CO2 storage cost.
Solar and wind power
The costs of solar and wind power in the model are determined by learning and depletion dynamics. For renewable energy, costs relate to capital, O&M and system integration. The capital costs mostly relate to learning and depletion processes. Learning is represented by in learning curves (Box 4.1.3.1); depletion is by long-term in cost–supply curves.
The additional system integration costs relate to curtailed electricity (if production exceeds demand and the overcapacity cannot be used within the system), backup capacity; and additional required spinning reserve. The last items are needed to avoid loss of power if the supply of wind or solar power drops suddenly, enabling a power scale up in a relatively short time, in power stations operating below maximum capacity (Hoogwijk, 2004).
To determine curtailed electricity, the model compares 10 points on the load-demand curve at the overlap between demand and supply. For both wind and solar power, a typical load supply curve is assumed (see Hoogwijk, 2004). If supply exceeds demand, the overcapacity in electricity is assumed to be discarded, resulting in higher production costs.
Because wind and solar power supply is intermittent (variable and thus not reliable), the model assumes that backup capacity needs to be installed. It is assumed that no backup is required for first 5% penetration of the intermittent capacity. However, for higher levels of penetration, the effective capacity (degree to which operators can rely on plants producing at a specific time) of intermittent resources is assumed to decrease. This is referred to as the capacity factor. This decrease leads to the need for backup power by low-cost options, such as gas turbines, the cost of which is allocated to the intermittent source.
The required spinning reserve of the power system is the capacity that can be used to respond to a rapid increase in demand. This is assumed to be 3.5% of the installed capacity of a conventional power plant. If wind and solar power further penetrate the market, the model assumes an additional, required spinning reserve of 15% of the intermittent capacity (after subtraction of the 3.5% existing capacity). The related costs are allocated to the intermittent source.
The costs of solar and wind power are the model determined by learning and depletion dynamics. For renewable energy, costs relate to capital, O&M and system integration. The capital costs mostly relate to learning and depletion processes (learning is represented by so-called learning curves; depletion is represented by long-term cost–supply curves).
The additional system integration costs relate to
- Discarded electricity in cases where production exceeds demand and the overcapacity cannot be used within the system;
- Back-up capacity;
- Additional required spinning reserve;
The two last items are needed to avoid loss of power if the supply of wind or solar power suddenly drops, enabling a power scale up in a relatively short time, in power stations operating below maximum capacity (Hoogwijk, 2004).
- To determine discarded electricity, the model makes a comparison between 10 different points on the load-demand curve, at the overlap between demand and supply. For both wind and solar power, a typical load–supply curve is assumed (see Hoogwijk, 2004). If supply exceeds demand, the overcapacity in electricity is assumed to be discarded, resulting in higher production costs.
- Because wind and solar power supply is intermittent (i.e. it varies and therefore is not reliable), the model assumes that so-called back-up capacity needs to be installed. For the first 5% penetration of the intermittent capacity, it is assumed that no-back is required. However, for higher levels of penetration, the effective capacity (i.e. degree to which operators can rely on plants producing at a particular moment in time) of intermittent resources is assumed to decrease (referred to as the capacity factor). This decrease leads to the need of back-up power(by low-cost options, such as gas turbines), the costs of which are allocated to the intermittent source.
- The required spinning reserve of the power system (capacity that can be used to respond to a rapid increase in demand) is assumed to be 3.5% of the installed capacity of a conventional power plant. If wind and solar power further penetrate the market, the model assumes an additional, required spinning reserve of 15% of the intermittent capacity (but after first subtracting the 3.5% existing capacity). The related costs are allocated to the intermittent source.
Nuclear power
For nuclear power, the costs also consists of capital, O&M and nuclear fuel costs. Similar to the renewable energy options, technology improvement nuclear power is described via a learning curve (so costs decrease with cumulative installed capacity). At the same time, fuel costs increase as a function of depletion. Fuel costs are determined on the basis of the estimated extraction costs of uranium and thorium resources, as is described in the component Energy supply. A small trade model for these fission fuels is included.
Hydrogen generation model
The structure of the hydrogen model is similar to that of the electric power model (Van Ruijven et al., 2007). There are, however, some important differences:
- The hydrogen model distinguishes the following 11 supply options: hydrogen production plants on the basis of coal, oil, natural gas and bio-energy, with and
without carbon capture and storage (8 plants), hydrogen production from electrolysis, direct hydrogen production from solar thermal processes, and, finally, small methane reform plants.
- For simplification, no description of preferences for different power plants is accounted for in the operational strategy. In other words, the load factor for each option equals the total production divided by the capacity for each region.
- Intermittence does not play an important role, as hydrogen can be stored to some degree. Therefore, there are no equations simulating system integration.
- Hydrogen can be traded. Therefore, a trade model is added, similar to the trade models for fossil fuels, as is described in the Energy supply section.
}}